Based on stereometry, depth information can be extracted from multiple 2D views of an object. At the least, two views can be utilized in the same way as to how our two eyes work with our brain to achieve depth perception. The same effect can be done using two cameras taking the two views of an object. Matching the image coordinates of the same point on the object will provide the derivation for the depth at that point. However, this task would be very tedious when trying to reconstruct for all the points on the object. An alternative way is by replacing one of the cameras with a projector. The pixels of the projector can act as the same pixels of the camera for matching of points with the other camera. A structured pattern can represent the points on the projector as it is projected on to the object.
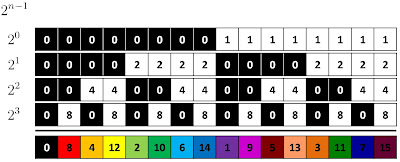
In this activity, binary codes (shown below) are used as patterns. The patterns differ by increasing the number of repetitions (cycles) of the black-white vertical strip sequence by a factor of 2. The algorithm relies on the fact that by adding these set of binary patterns multiplied by 2^(n-1), where n is the number of cycles, a unique number is obtained for each vertical strip in the added image. This is demonstrated on the diagram below, where the sum of the binary patterns (black and white strips) results into an array of unique values. This can represent the unique points on the projector that can be matched when this set of patterns is imaged by the camera.
Initially, the patterns are projected on a reference plane and then imaged to determine the points on the camera.
Upon placing the 3D object, the vertical strips would be displaced from their initial position.
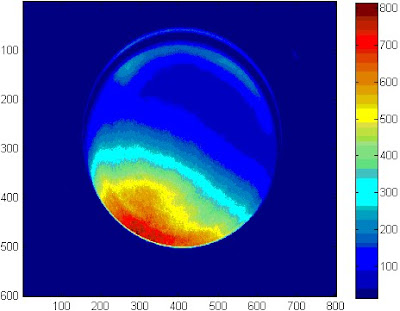
The amount of shift can be determined by how many pixels that the corresponding number of that strip has been displaced from its initial position in the reference plane image. This can, then, be easily related to the depth of the object, allowing 3D reconstruction of the object:
(To be continued)

Initially, the patterns are projected on a reference plane and then imaged to determine the points on the camera.
Upon placing the 3D object, the vertical strips would be displaced from their initial position.
The amount of shift can be determined by how many pixels that the corresponding number of that strip has been displaced from its initial position in the reference plane image. This can, then, be easily related to the depth of the object, allowing 3D reconstruction of the object:
(To be continued)